Back

The Fool's Sequence

A fool’s number is a number with digits comprised only of 69 and 420. This program can find the nth fool’s number, when sorted in increasing order.

Growth

A fools number can be formed by appending 69 or 420 to another smaller fool number. As such, if \(d_i\) is the number of fool numbers with \(i>3\) digits, then \(d_i=d_{i-2}+d_{i-3}\) (we can define \(d_3=1,d_2=1,d_1=0\)).

The asymtotic growth of \(d_n\) can be found with function \(x^3=1+x\), which gives \(x≈1.3247, d_n≈1.3247^n\)

Then the number of digits with \(n\) or fewer digits is \(s_n=\sum_{i=1}^n d_i=\theta(1.3247^n)\)

Of course, the \(s_n\)th number has \(n\) digits so it is approximately \(10^n\). The \(n\)th fool number is \(\theta(10^{\log_{1.3247}n })=\theta(n^{8.18})\)

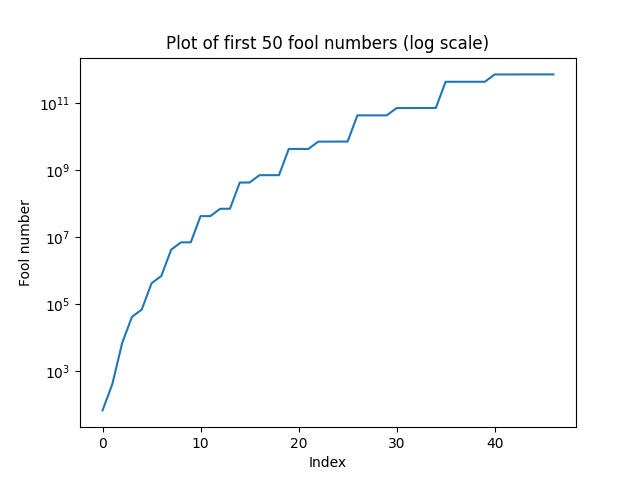
It’s a self similar fractal.

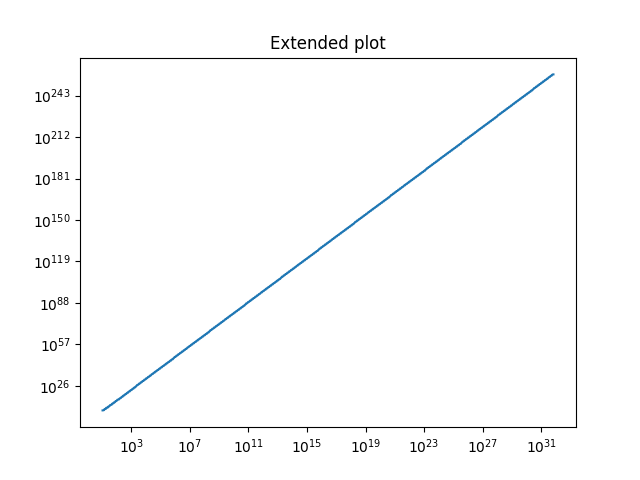
First few terms: 69 420 6969 42069 69420 420420 696969 4206969 6942069 6969420 42042069 42069420 69420420 69696969 420420420 420696969 694206969 696942069 696969420 4204206969 4206942069 4206969420 6942042069 6942069420 6969420420 6969696969 42042042069 42042069420 42069420420 42069696969 69420420420 69420696969 69694206969 69696942069 69696969420 420420420420 420420696969 420694206969 420696942069 420696969420 694204206969 694206942069 694206969420 696942042069 696942069420 696969420420 696969696969